Floor Stand Touch Screen Query Kiosk,interactive information kiosks,IR touch inquiry machine HuiZhou GreenTouch Technology Co.,Ltd , https://www.bbstouch.com
Negative resistance track and op amp in circuit foundation
I posed a simple thinking question, but it involved some fundamental concepts. The knowledge required is basic (secondary undergraduate level), yet no one has analyzed it in depth. Here, I will provide a detailed explanation and introduce another example to help clarify the topic.
First, let me reference the original post:
[http://bbs.21ic.com/icview-1623966-1-1.html](http://bbs.21ic.com/icview-1623966-1-1.html)
The image below shows the initial setup:

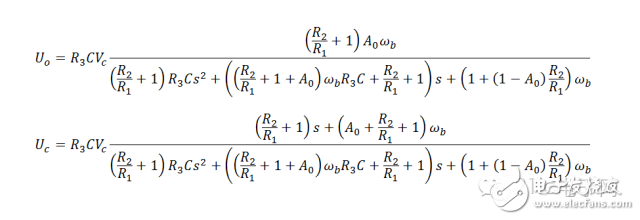
At this point, it might seem like we have a "solution," but for deeper analysis, we need to look at the system's characteristic roots (poles). Let’s examine the following equations:

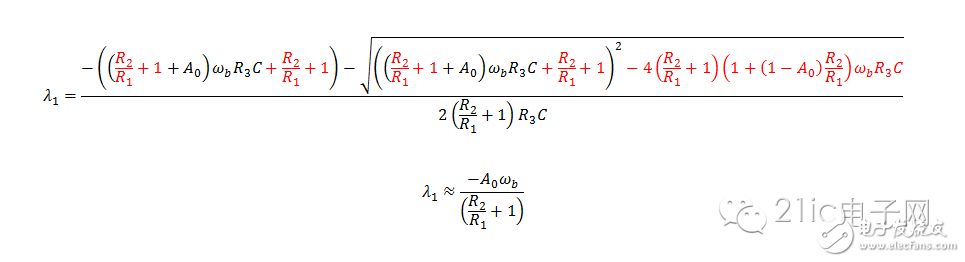
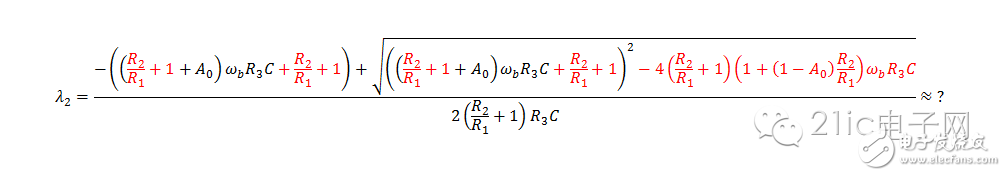
If we ignore the "red word" in the equation, the result becomes zero, which is clearly incorrect. In reality, this represents an indeterminate form: infinity minus infinity.
Let’s change the approach slightly:
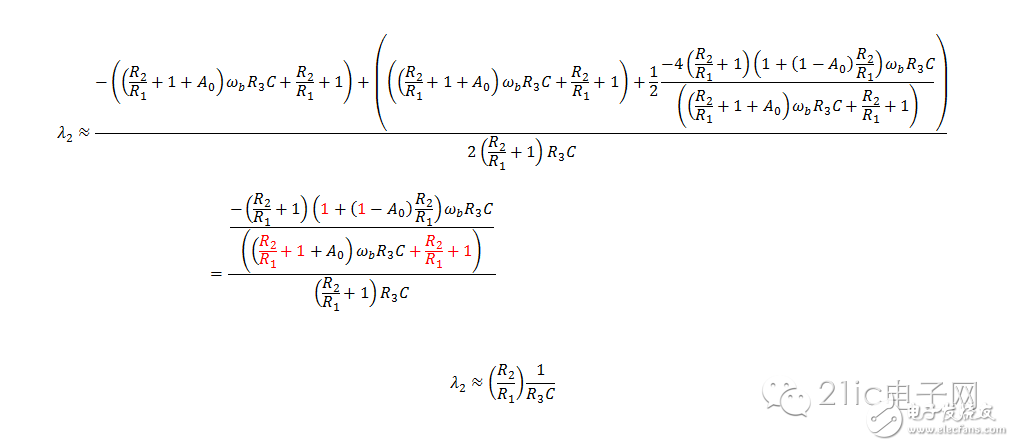
This time, it works!
After applying a limit approximation, we find two characteristic roots (poles):
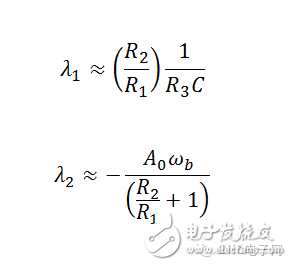
Note that the first root is **limited**, while the second tends toward **negative infinity**.
Next, we perform partial fraction decomposition to determine the exact form of the motion trajectory:

By comparing previous formulas, we can set up the following equations and solve them:

Using extreme approximations, we get:

Now, we obtain the final expression:


The parameter (t) equation is given above, and here is the direct relationship:
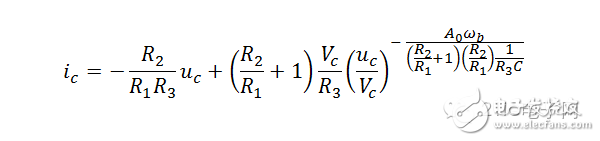
Now, let’s look at the trajectory map:

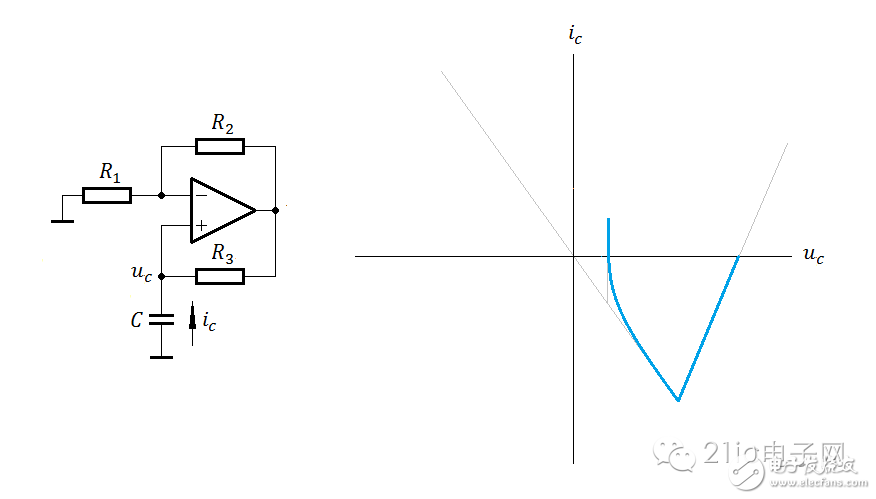
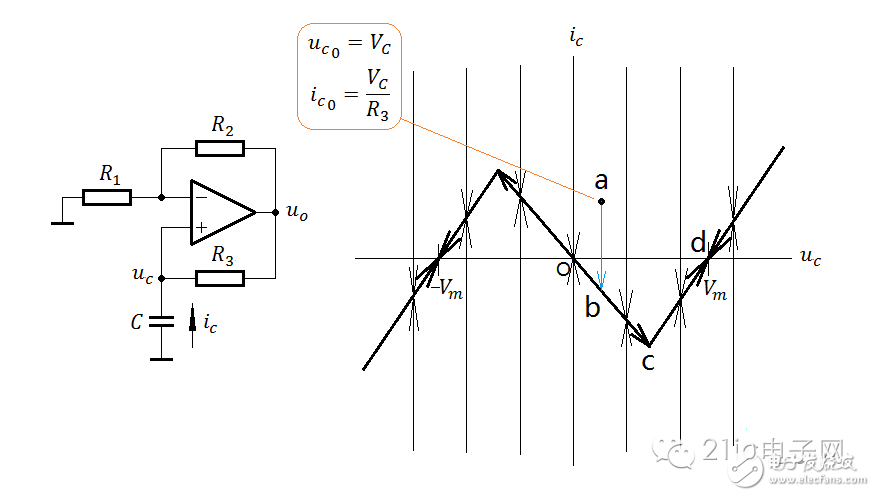
This figure illustrates the direction of state transitions and provides a clear and intuitive representation of the system’s behavior. You can choose any initial point and draw the corresponding trajectory.
To further illustrate the limiter section, here are a few more formulas:

For this example, here are a few key points:
1. This example visually demonstrates the concept of "negative resistance," specifically the negative resistance trajectory under stable conditions.
2. Starting from any non-zero initial point, the system moves toward one of the two state endpoints, making oscillation impossible.
3. The negative resistance line seems to act like a gravitational force, instantly pulling any state point not on the line toward it, provided the operational amplifier is not saturated.
Now, let’s look at another example:


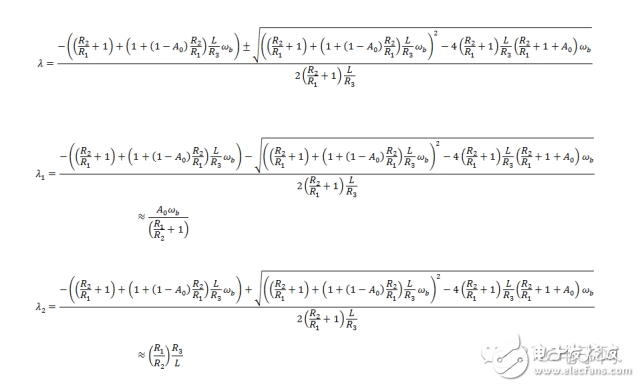
**Pay attention to the characteristic root that tends toward infinity!**
Correspondingly, here are a few expressions:

**Note the index item of the red line.**
Here is the trajectory map for the second case:
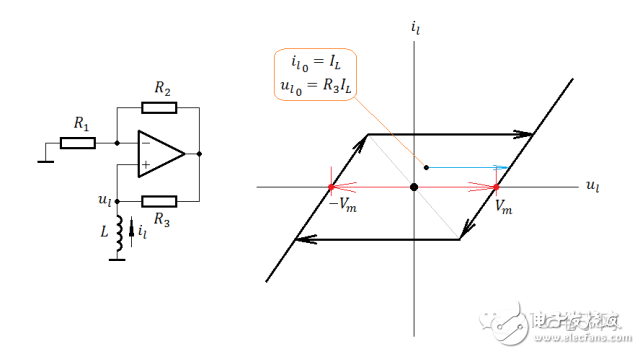
As shown, the op-amp input voltage exceeds the limit voltage.
Again, here are a few key points for this example:
1. If the system is unstable, there is no "negative resistance" at all, because the negative resistance path doesn’t exist.
2. Starting from any non-zero initial point, the system is quickly pulled toward one of the limiter lines and then cycles along the trajectory, allowing for oscillation.
3. The original "negative resistance line" becomes a line of unstable equilibrium points. Any state point above it (which statistically occurs with zero probability) will eventually move away due to disturbances.
Finally, considering the purpose of this post and the original question, it’s important to emphasize the role of circuit theory as a foundation. Although nonlinear systems are involved, linear analysis in circuit theory serves as the simplest form of piecewise linearization. When linearization isn't possible, nonlinear analysis must be used, which is a completely different domain. However, without a solid understanding of basic linear analysis, moving into nonlinear analysis would be like trying to build a house without a foundation.
**Therefore, I strongly recommend that students or beginners take their circuit theory courses seriously. Without this foundation, it’s difficult to progress further in more advanced topics.**
Our infrared touch-screen kiosk supports Windows and Linux operating systems, has excellent functionality and flexibility, and provides you with reliable industrial or commercial solutions. It can easily integrate your industrial automation system to achieve simple human-computer interaction and seamlessly connect the interactive experience. These (27-inch to 55-inch) kiosks can be as simple as inserting a USB or SD media card to display your creative advertising, or they can be connected to the Internet to allow users to search for themselves on the Touch Screen. Interactive terminals are mainly used in public places such as trade shows, shopping malls, restaurants, airports, etc. We can also provide customized services according to your needs.